Suslin theorem

(in descriptive set theory)

There exists an 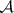-set (of the number axis ) that is not a Borel set.

In order that a given 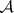-set be a Borel set it is necessary and sufficient that its complement also be an -set.

Every 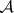-set in the -dimensional space is the (orthogonal) projection of a Borel set (even of type 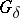) in (and consequently, a plane Borel set of type 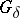exists whose projection is not a Borel set); the projection of an 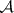-set is an 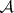-set.

All these results were obtained by M.Ya. Suslin [1]. In order to define an 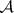-set, he used the -operation, while other methods of defining 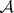-sets were discovered subsequently. The -operation was in fact first discovered by P.S. Aleksandrov [2], who demonstrated (although he did not explicitly formulate it) that every Borel set can be obtained as the result of the 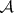-operation over closed sets (and is consequently an 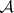-set), and used this to prove a theorem on the cardinality of Borel sets (in fact, of -sets) in 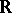. N.N. Luzin subsequently posed the question of the existence of an -set that is not a Borel set. Theorem 1) answered this question. Theorems 1) and 2) were put forward by Suslin without proof [1]. Suslin did subsequently prove them, but it was not until Luzin simplified the proofs that they were published. In order to prove 1), Suslin constructed a plane 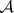-set that was universal for all Borel sets and examined the set of its points that lie on the diagonal 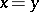(see [3], p. 94). Theorem 2) is now often called the Suslin criterion for Borel sets. 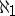Suslin's proof of this theorem was based on a decomposition of a -set into the sum of Borel sets (see [4], [5]).

References

[1]	M. [M.Ya. Suslin] Souslin, "Sur une définition des ensembles mesurables sans nombres transfinis" C.R. Acad. Sci. Paris , 164 (1917) pp. 88–91
[2]	P.S. [P.S. Aleksandrov] Alexandroff, "Sur la puissance des ensembles mesurables 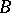" C.R. Acad. Sci. Paris , 162 (1916) pp. 323–325
[3]	L.V. Keldysh, P.S. Novikov, "The work of N.N. Luzin in the domain of the descriptive theory of sets" Uspekhi Mat. Nauk , 8 : 2 (1953) pp. 93–104 (In Russian)
[4]	N.N. Luzin, "Collected works" , 2 , Moscow (1958) (In Russian)
[5]	F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978))

Comments

For a more comprehensive historical note on 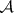-sets (also called analytic sets) see Rogers' contribution in [a1]. In particular, Suslin's work began with the discovery of a mistake in a famous paper of H. Lebesgue (1905), which also had a big positive influence on the construction of the first tools of descriptive set theory (universal sets, 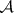-operation, etc.). The theorem on the cardinality of Borel sets proved by Aleksandrov, was independently proved by F. Hausdorff [a2] (in a similar manner). Suslin's theorem 2) is now considered to be a corollary of the first separation theorem (see Luzin separability principles). It has a more powerful version in effective descriptive set theory (see (the comments to) Descriptive set theory), called the Suslin–Kleene theorem: A set is hyper-arithmetic (roughly speaking, is an effective Borel set) if and only if it belongs to 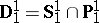(roughly speaking, is an effective analytic and co-analytic set).

References

[a1]	C.A. Rogers, J.E. Jayne, C. Dellacherie, F. Tøpsoe, J. Hoffman-Jørgensen, D.A. Martin, A.S. Kechris, A.H. Stone, "Analytic sets" , Acad. Press (1980)
[a2]	F. Hausdorff, "Die Mächtigkeit der Borelschen Mengen" Math. Ann. , 77 (1916) pp. 430–437
[a3]	Y.N. Moschovakis, "Descriptive set theory" , North-Holland (1980)