Interior
From Encyclopedia of Mathematics
The set of all points 
of a subset 
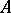of a topological space 
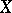for which an open set 
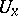in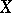 
exists such that 
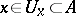. The interior of the set 
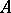is usually denoted by 
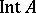and represents the largest open set in 
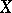contained in 
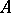. The equality 
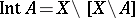holds, where 
denotes closure in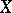 
. The interior of a set in a topological space 
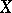is a regular open or canonical set. Spaces in which the open canonical sets form a base for the topology are called semi-regular. Every regular space is semi-regular. The interior is sometimes called the open kernel of the set.
Comments
See also Interior of a set.
How to Cite This Entry:
Interior. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Interior&oldid=33639
Interior. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Interior&oldid=33639
This article was adapted from an original article by V.I. Ponomarev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article