Complete Riemannian space
A Riemannian space with its internal distance function  that is complete as a metric space with metric
that is complete as a metric space with metric  .
.
Let  be a connected Riemannian space with its Levi-Civita connection, then the following three assertions are equivalent: a)
be a connected Riemannian space with its Levi-Civita connection, then the following three assertions are equivalent: a)  is complete; b) for each point
is complete; b) for each point  the exponential mapping
the exponential mapping  is defined on all of
is defined on all of  (where
(where  is the tangent space to
is the tangent space to  at
at 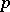 ); and c) every closed set
); and c) every closed set 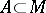 that is bounded with respect to the distance
that is bounded with respect to the distance 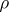 is compact (the Hopf–Rinow theorem). Consequences are: Any two points
is compact (the Hopf–Rinow theorem). Consequences are: Any two points  in a complete Riemannian space
in a complete Riemannian space  can be joined in
can be joined in 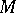 by a geodesic of length
by a geodesic of length 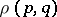 ; any geodesic is indefinitely extendable.
; any geodesic is indefinitely extendable.
There is a generalization [2] of this theorem to the case of a space with a non-symmetric distance function.
References
| [1] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
| [2] | S.E. Cohn-Vossen, "Existenz kürzester Wege" Compos. Math. , 3 (1936) pp. 441–452 |
Comments
Let 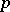 be a point of the Riemannian manifold
be a point of the Riemannian manifold 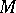 . Then
. Then 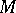 is called geodesically complete at
is called geodesically complete at 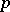 if
if  is defined on all of
is defined on all of 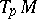 , and
, and 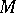 is geodesically complete if this is the case at all
is geodesically complete if this is the case at all 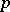 . For
. For 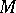 to be complete (or, equivalently, geodesically complete) it suffices that
to be complete (or, equivalently, geodesically complete) it suffices that 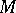 is geodesically complete at one point.
is geodesically complete at one point.
References
| [a1] | W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German) |
Complete Riemannian space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Complete_Riemannian_space&oldid=33636