Core of a subgroup
From Encyclopedia of Mathematics
Let 
be a subgroup of 
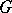. The core of 
is the maximal subgroup of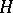 
that is normal in 
(cf. also Normal subgroup). It follows that
 |
If the index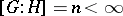 
, then 
divides 
.
Let 
and define the permutation representation of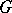 
on the set of right cosets of 
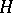in 
. Then its kernel is the core of 
in 
.
References
| [a1] | M. Suzuki, "Group theory" , I , Springer (1982) |
| [a2] | W.R. Scott, "Group theory" , Dover, reprint (1987) (Original: Prentice-Hall, 1964) |
How to Cite This Entry:
Core of a subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Core_of_a_subgroup&oldid=33614
Core of a subgroup. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Core_of_a_subgroup&oldid=33614
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article