Lobatto quadrature formula
From Encyclopedia of Mathematics
A quadrature formula of highest algebraic degree of accuracy for the interval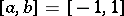 
and weight 
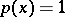with two fixed nodes: the end-points of 
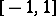. The Lobatto quadrature formula has the form
 |
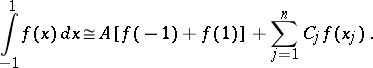The points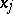 
are the roots of the polynomial 
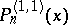(a Jacobi polynomial), orthogonal on 
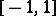with respect to the weight 
, 
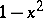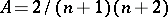and 
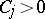. The algebraic degree of accuracy is 
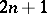. A table of nodes and coefficients of the Lobatto quadrature formula for 
(
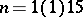varies from 1 to 15 with step 1) was given in [2] (see also [3]).
The formula was established by R. Lobatto (see [1]).
References
| [1] | R. Lobatto, "Lessen over de differentiaal- en integraalrekening" , 1–2 , 's Gravenhage (1851–1852) |
| [2] | V.I. Krylov, "Approximate calculation of integrals" , Macmillan (1962) (Translated from Russian) |
| [3] | H.H. Michels, "Abscissas and weight coefficients for Lobatto quadrature" Math. Comp. , 17 (1963) pp. 237–244 |
Comments
For the notion of algebraic degree of accuracy of a quadrature formula see Quadrature formula.
References
| [a1] | A.H. Stroud, "Gaussian quadrature formulas" , Prentice-Hall (1966) |
How to Cite This Entry:
Lobatto quadrature formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lobatto_quadrature_formula&oldid=33608
Lobatto quadrature formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lobatto_quadrature_formula&oldid=33608
This article was adapted from an original article by I.P. Mysovskikh (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article