Reynolds number
From Encyclopedia of Mathematics
One of the non-dimensional numbers which provide criteria of similarity for flows of viscous liquids and gases. It characterizes the relation between the inertial forces and the forces of viscosity:
 |
where 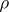 is the density,
is the density, 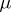 is the dynamical coefficient of viscosity of the liquid or gas,
is the dynamical coefficient of viscosity of the liquid or gas,  is the typical rate of flow, and
is the typical rate of flow, and 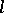 is the typical linear dimension.
is the typical linear dimension.
The Reynolds number also determines the mode of flow of a liquid in terms of a critical Reynolds number, 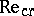 . When
. When  , only laminar liquid flow is possible, whereas when
, only laminar liquid flow is possible, whereas when 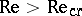 the flow may become turbulent.
the flow may become turbulent.
The Reynolds number is named after O. Reynolds.
Comments
References
| [a1] | G.K. Batchelor, "An introduction to fluid dynamics" , Cambridge Univ. Press (1974) pp. Sect. 4.7 |
| [a2] | M.I. Vishik, A.V. Fursikov, "Mathematical problems of statistical hydromechanics" , Kluwer (1988) pp. Chapts. 3; 4; 6 (Translated from Russian) |
| [a3] | L.D. Landau, E.M. Lifshitz, "Fluid mechanics" , Pergamon (1959) (Translated from Russian) |
How to Cite This Entry:
Reynolds number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reynolds_number&oldid=33592
Reynolds number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Reynolds_number&oldid=33592
This article was adapted from an original article by Material from the article "Reynolds number" in BSE-3 (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article