Gauss semi-group

A commutative semi-group with unit satisfying the cancellation law, in which any non-invertible element is decomposable into a product of irreducible elements (i.e. elements that cannot be represented as a product of non-invertible factors); moreover, for each two such decompositions

one has 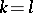and, possibly after renumbering the factors, also

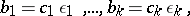where are invertible elements. Typical examples of Gauss semi-groups include the multiplicative semi-group of non-zero integers, and that of non-zero polynomials in one unknown over a field. Any two elements of a Gauss semi-group have a highest common divisor.

References

[1]	A.G. Kurosh, "Lectures on general algebra" , Chelsea (1963) (Translated from Russian)