Iterated kernel

A function 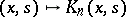that is formed from the given kernel of an integral operator (cf. Kernel of an integral operator)

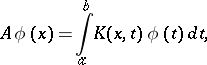by the recurrence relations

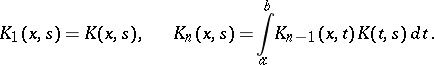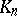is called the -th iterate, or -th iterated kernel, of 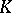. An iterated kernel is sometimes called a repeated kernel. If is a continuous or square-integrable kernel, then all its iterates are continuous, respectively, square integrable. If 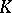is a symmetric kernel, so are all its iterates. The kernel 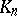is the kernel of the operator 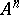. The equality

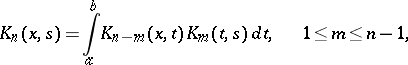holds.

References

[1]	V.I. Smirnov, "A course of higher mathematics" , 4 , Addison-Wesley (1964) pp. Chapt. 1 (Translated from Russian)
[2]	S.G. Mikhlin, "Linear integral equations" , Hindushtan Publ. Comp. , Delhi (1960) (Translated from Russian)

References

[a1]	I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1981)
[a2]	P.P. Zabreiko (ed.) A.I. Koshelev (ed.) M.A. Krasnoselskii (ed.) S.G. Mikhlin (ed.) L.S. Rakovshchik (ed.) V.Ya. Stet'senko (ed.) T.O. Shaposhnikova (ed.) R.S. Anderssen (ed.) , Integral equations - a reference text , Noordhoff (1975) (Translated from Russian)