Lebesgue theorem

Lebesgue's theorem in dimension theory: For any 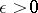the -dimensional cube has a finite closed -covering of multiplicity 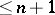, and at the same there is an 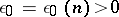such that any finite closed 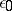-covering of the -dimensional cube has multiplicity 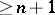(cf. also Covering (of a set)). This assertion led later to a definition of a fundamental dimension invariant, the Lebesgue dimension 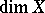of a normal topological space .

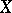Comments

This theorem is also called the Lebesgue covering theorem or "PflastersatzPflastersatz" (see Dimension). In the language of dimension theory it says that 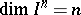for every .

References

[a1]	R. Engelking, "Dimension theory" , North-Holland & PWN (1978) pp. 19; 50 MR0482696 MR0482697 Zbl 0401.54029
[a2]	W. Hurevicz, G. Wallman, "Dimension theory" , Princeton Univ. Press (1948) ((Appendix by L.S. Pontryagin and L.G. Shnirel'man in Russian edition.))
[a3]	C. Kuratowski, "Introduction to set theory and topology" , Pergamon (1972) (Translated from Polish) MR0346724 Zbl 0267.54002 Zbl 0247.54001

Lebesgue's theorem on the passage to the limit under the integral sign: Suppose that on a measurable set 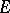there is specified a sequence of measurable functions 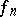that converges almost-everywhere (or in measure) on 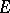to a function 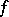. If there is a summable functi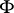on on 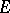such that for all and ,

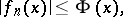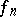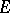then and are summable on and

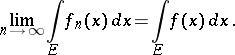This was first proved by H. Lebesgue [1]. The important special case when 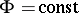and has finite measure is also called the Lebesgue theorem; he obtained it earlier [2].

A theorem first proved by B. Levi [3] is sometimes called the Lebesgue theorem: Suppose that on a measurable set 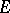there is specified a non-decreasing sequence of measurable non-negative functions 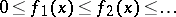(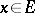) and that

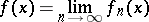almost-everywhere; then

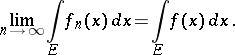References

[1]	H. Lebesgue, "Sur les intégrales singuliéres" Ann. Fac. Sci. Univ. Toulouse Sci. Math. Sci. Phys. , 1 (1909) pp. 25–117 MR1508308 Zbl 41.0329.01 Zbl 41.0327.02
[2]	H. Lebesgue, "Intégrale, longueur, aire" , Univ. Paris (1902) (Thesis) Zbl 33.0307.02
[3]	B. Levi, "Sopra l'integrazione delle serie" Rend. Ist. Lombardo sue Lett. (2) , 39 (1906) pp. 775–780 Zbl 37.0424.03
[4]	S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) MR0167578 Zbl 1196.28001 Zbl 0017.30004 Zbl 63.0183.05
[5]	I.P. Natanson, "Theory of functions of a real variable" , 1–2 , F. Ungar (1955–1961) (Translated from Russian) MR0640867 MR0354979 MR0148805 MR0067952 MR0039790

T.P. Lukashenko

Comments

This Lebesgue theorem is also called the dominated convergence theorem, while Levi's theorem is also known as the monotone convergence theorem.

References

[a1]	N. Dunford, J.T. Schwartz, "Linear operators" , 1–3 , Interscience (1958–1971) MR1009164 MR1009163 MR1009162 MR0412888 MR0216304 MR0188745 MR0216303 MR1530651 MR0117523 Zbl 0635.47003 Zbl 0635.47002 Zbl 0635.47001 Zbl 0283.47002 Zbl 0243.47001 Zbl 0146.12601 Zbl 0128.34803 Zbl 0084.10402
[a2]	P.R. Halmos, "Measure theory" , v. Nostrand (1950) MR0033869 Zbl 0040.16802
[a3]	E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) MR0188387 Zbl 0137.03202