Closure of a computational algorithm

A system of equations

(1)

obtained as the limit as , of a system of partially solved equations

(2)

describing the successive steps of a computational algorithm for the solution of an equation

(3)

(for example, a finite-difference equation, in which case 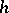is the grid spacing), which approximates the equation

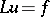(4)

as . It is assumed here that 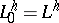, , is the identity operator, and that , i.e. the 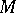-th step of the algorithm yields a final solution of the approximate equation (3). The function is assumed to increase with 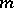(e.g. is a linearly increasing function) and to satisfy the boundary conditions 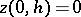, 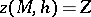. The case 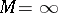is admissible; then 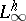, , 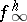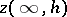are interpreted as the limits of the variable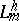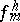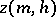s , , as 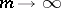. The case 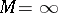corresponds to iteration methods for solving equation (3).

If the operators in equation (1) are uniformly bounded in , one says that algorithm (2) admits a regular closure. Although the set of algorithms with regular closure does not coincide with the set of actually stable algorithms, construction of a closed algorithm frequently helps in investigating the stability of an algorithm under various perturbations (in particular computational errors) (see [3], [4]).

The concept of a closed algorithm was introduced in [1]. There the closure of an algorithm for successive elimination of unknowns, when solving finite-difference equations that approximate an equation (4) with 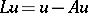, where 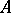is a Fredholm integral operator, was obtained and investigated.

The construction of the closure of an algorithm and the inverse operation — the construction of a discrete algorithm the closure of which is a given continuous process — proves useful in designing new methods for the solution of problems. In particular, a large number of iteration methods admit closures which are steady processes. For example, the simple iteration method for the solution of the Laplace difference equation corresponds to the steady process 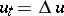; and the two-step iteration method corresponds to the steady process 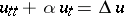, (see [5]).

References

[1]	S.L. Sobolev, "Some remarks on the numerical solution of integral equations" Izv. Akad. Nauk SSSR Ser. Mat. , 20 : 4 (1956) pp. 413–436 (In Russian)
[2]	I. [I. Babushka] Babuška, M. Práger, E. Vitásek, "Closure of computational processes and the double-sweep method" Zh. Vychisl. Mat. i Mat. Fiz. , 4 : 2 (1964) pp. 351–353 (In Russian)
[3]	N.S. Bakhalov, "Computational methods for the solution of ordinary differential equations" , Kiev (1970) (In Russian)
[4]	N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian)
[5]	V.K. Saul'ev, "Integration of equations of parabolic type by the method of nets" , Pergamon (1964) (Translated from Russian)
[6]	A.F. Shapkin, "Closure of two computational algorithms, based on the idea of orthogonalization" Zh. Vychisl. Mat. i Mat. Fiz. , 7 : 2 (1967) pp. 411–416 (In Russian)

References

[a1]	I. [I. Babushka] Babuška, M. Práger, E. Vitásek, "Numerical processes in differential equations" , Wiley (1966)