Beurling theorem
From Encyclopedia of Mathematics
Let 
be a function in the Hardy class 
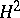(cf. also Hardy classes). The vector space spanned by the functions 
, 
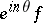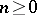, is dense in 
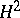if and only if 
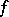is an outer function (cf. also Hardy classes).
This follows from the characterization of closed shift-invariant subspaces in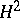 
as being of the form 
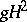with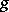 
an inner function.
See Beurling–Lax theorem for further developments.
References
| [a1] | B. Sz.-Nagy, C. Foias, "Harmonic analysis of operators on Hilbert spaces" , North-Holland (1970) pp. 104 |
| [a2] | B. Beauzamy, "Introduction to operator theory and invariant subspaces" , North-Holland (1988) pp. 194 |
| [a3] | W. Mlak, "Hilbert spaces and operator theory" , Kluwer Acad. Publ. (1991) pp. 188; 190 |
How to Cite This Entry:
Beurling theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Beurling_theorem&oldid=33509
Beurling theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Beurling_theorem&oldid=33509
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article