Enumerable predicate
An arithmetic predicate 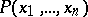 is called enumerable relative to a given formal system
is called enumerable relative to a given formal system 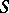 of arithmetic if it has the following property: There is a formula
of arithmetic if it has the following property: There is a formula 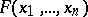 in the language of formal arithmetic (cf. Arithmetic, formal) such that for any natural numbers
in the language of formal arithmetic (cf. Arithmetic, formal) such that for any natural numbers 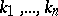 ,
,
1) if 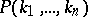 is true, then
is true, then 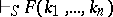 ;
;
2) if 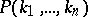 is false, then
is false, then 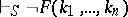 , where
, where 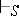 means derivability in
means derivability in 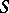 and
and 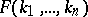 is the result of substituting in
is the result of substituting in 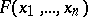 for the variables
for the variables  terms representing the numbers
terms representing the numbers 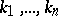 . In this case one says that the formula
. In this case one says that the formula 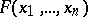 is an enumerability predicate for
is an enumerability predicate for 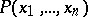 . For a formal system
. For a formal system 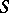 of arithmetic the following proposition holds: All recursive predicates, and only they, are enumerability predicates in
of arithmetic the following proposition holds: All recursive predicates, and only they, are enumerability predicates in  .
.
An  -place arithmetic function
-place arithmetic function  is called enumerable if there is an arithmetic formula
is called enumerable if there is an arithmetic formula 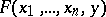 such that for any natural numbers
such that for any natural numbers 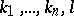 ,
,
1) if 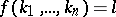 , then
, then 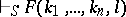 ;
;
2) 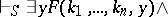
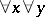
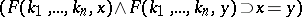 .
.
In the ordinary formal system of arithmetic all general recursive functions, and only they, are enumerable (cf. General recursive function).
References
| [1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1951) |
Comments
Predicates 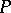 (functions
(functions 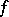 ) satisfying 1), 2) are more commonly called definable in the system
) satisfying 1), 2) are more commonly called definable in the system 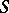 .
.
Enumerable predicate. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Enumerable_predicate&oldid=33501