Univalency radius

radius of univalence

The radius 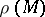of the largest disc 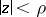in which all functions of the form

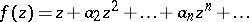belonging to the family of functions that are regular in the disc 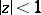satisfying 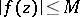for 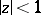are univalent. It turns out that

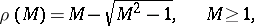and the function

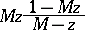is univalent in the disc 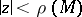, but not in any larger disc (with centre at the origin). For functions regular in the disc 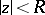and such that 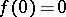, , 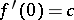, and 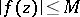, the radius of univalence is defined similarly, and its value can be easily obtained from .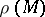

Comments

Cf. also Univalency conditions; Univalent function.

References

[a1]	P.L. Duren, "Univalent functions" , Springer (1983) pp. Sect. 10.11
[a2]	A.W. Goodman, "Univalent functions" , 2 , Mariner (1983)
[a3]	E. Landau, "Der Picard–Schottkysche Satz und die Blochse Konstante" Sitzungsber. Akad. Wiss. Berlin Phys. Math. Kl. (1925) pp. 467–474