Semi-perfect ring
A ring over which every finitely-generated left (or every finitely-generated right) module has a projective covering. A ring  with Jacobson radical
with Jacobson radical  is a semi-perfect ring if and only if
is a semi-perfect ring if and only if  is semi-local and if every idempotent of the quotient ring
is semi-local and if every idempotent of the quotient ring  has an idempotent pre-image in
has an idempotent pre-image in  . The first condition can be replaced by the requirement of classical semi-simplicity of the quotient ring
. The first condition can be replaced by the requirement of classical semi-simplicity of the quotient ring 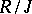 (cf. Classical semi-simple ring), and the second by the possibility of "lifting" modular direct decompositions from
(cf. Classical semi-simple ring), and the second by the possibility of "lifting" modular direct decompositions from  to
to  . A semi-perfect ring may also be characterized by the condition that every module admits a direct decomposition with respect to which the maximal direct summands are complemented. A ring of matrices over a semi-perfect ring is a semi-perfect ring.
. A semi-perfect ring may also be characterized by the condition that every module admits a direct decomposition with respect to which the maximal direct summands are complemented. A ring of matrices over a semi-perfect ring is a semi-perfect ring.
See also Perfect ring, and the references to that article.
Comments
Cf. also Projective covering.
References
| [a1] | L.H. Rowen, "Ring theory" , 1 , Acad. Press (1988) pp. 217 |
Semi-perfect ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Semi-perfect_ring&oldid=33494