Riemann summation method

A method for summing series of numbers. A series 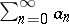can be summed by Riemann's method to a number 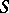if

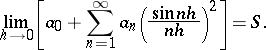This method was first introduced and its regularity was first proved by B. Riemann in 1854 (see [1]). The Riemann summation method has been applied in the theory of trigonometric series, where it is usually stated as follows: A trigonometric series

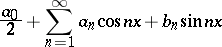with bounded coefficients 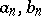can be summed by Riemann's method at a point 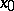to a number 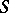if the function

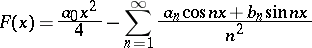has, at 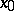, Riemann derivative equal to .

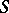References

[1]	B. Riemann, "Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe" , Gesammelte Math. Abhandlungen , Dover, reprint (1957) pp. 227–264
[2]	N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian)
[3]	A. Zygmund, "Trigonometric series" , 1–2 , Cambridge Univ. Press (1988)
[4]	G.H. Hardy, "Divergent series" , Clarendon Press (1949)

Comments

Regularity (cf. Regular summation methods) is expressed by Riemann's first theorem; the theorem stated above is called Riemann's second theorem. The function 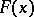is also called the Riemann function.

References

[a1]	W. Beekman, "Theorie der Limitierungsverfahren" , Springer (1970)