Halphen pencil

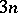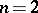A pencil of plane algebraic curves of degree with nine -tuple basis points. Such pencils were first studied by G. Halphen [1] for . The basis points 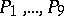of a Halphen pencil, which may also include infinitely near points, always lie on a cubic curve 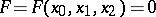. An arbitrary curve from the Halphen pencil has the equation 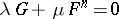, where 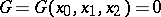is an elliptic curve of degree 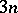with singular points 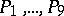of multiplicity . If 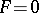is a non-singular curve, then, with respect to the group law on this curve, 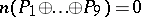. This fact can be generalized to the case when 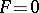is a curve with singular points [3]. Each pencil of elliptic curves on a plane may be transformed, by a birational transformation of the plane, into a Halphen pencil [2], [3].

References

[1]	G.H. Halphen, "Sur les courbes planes du sixième degré à neuf points double" Bull. Soc. Math. France , 10 (1882) pp. 162–172
[2]	E. Bertini, Ann. Mat. Pura Appl. , 8 (1877) pp. 224–286
[3]	I.V. Dolgachev, "On rational surfaces with a pencil of elliptic curves" Izv. Akad. Nauk SSSR Ser. Mat. , 30 (1966) pp. 1073–1100 (In Russian)