Hermitian structure
on a manifold 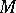
A pair 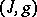 consisting of a complex structure
consisting of a complex structure 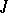 on
on 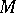 and a Hermitian metric
and a Hermitian metric 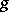 in the tangent space
in the tangent space 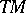 , that is, a Riemannian metric
, that is, a Riemannian metric 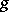 that is invariant under
that is invariant under 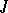 :
:
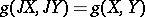 |
for any vector fields 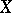 and
and 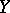 on
on 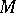 . A Hermitian structure specifies in any tangent space
. A Hermitian structure specifies in any tangent space 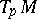 the structure of a Hermitian vector space (see Hermitian metric). A manifold with a Hermitian structure is called a Hermitian manifold. A Hermitian structure defines on
the structure of a Hermitian vector space (see Hermitian metric). A manifold with a Hermitian structure is called a Hermitian manifold. A Hermitian structure defines on 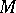 a differential
a differential  -form
-form 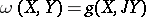 , which is called the canonical
, which is called the canonical  -form of the Hermitian manifold. Any structure
-form of the Hermitian manifold. Any structure 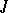 on
on  can be completed by some Riemannian metric
can be completed by some Riemannian metric 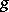 to a Hermitian structure
to a Hermitian structure 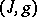 : for
: for 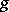 one can take the metric
one can take the metric 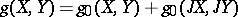 , where
, where 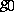 is an arbitrary metric. The canonical Hermitian connection of a Hermitian metric
is an arbitrary metric. The canonical Hermitian connection of a Hermitian metric 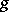 can be regarded as an affine connection with torsion
can be regarded as an affine connection with torsion 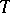 on
on 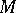 relative to which the fields
relative to which the fields 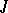 and
and 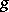 are parallel. Among all affine connections satisfying these conditions it is uniquely characterized by the identity
are parallel. Among all affine connections satisfying these conditions it is uniquely characterized by the identity 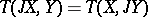 , which is valid for its torsion tensor
, which is valid for its torsion tensor 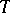 and any vector fields
and any vector fields 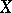 and
and 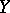 . The curvature tensor
. The curvature tensor 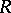 of the canonical connection satisfies the condition
of the canonical connection satisfies the condition 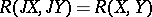 . A Hermitian manifold is a Kähler manifold if and only if the canonical Hermitian connection has no torsion and hence is the same as the Levi-Civita connection of
. A Hermitian manifold is a Kähler manifold if and only if the canonical Hermitian connection has no torsion and hence is the same as the Levi-Civita connection of 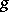 .
.
A natural generalization of the concept of a Hermitian structure is that of an almost-Hermitian structure, which is a pair 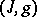 consisting of an almost-complex structure
consisting of an almost-complex structure 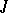 on
on 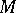 and a Riemannian metric
and a Riemannian metric 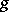 that is invariant under
that is invariant under 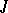 . If the fundamental
. If the fundamental  -form
-form 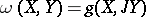 is closed, then an almost-Hermitian structure is called almost Kählerian. The specification of an almost-Hermitian structure is equivalent to a reduction of the structure group of the tangent bundle to the group
is closed, then an almost-Hermitian structure is called almost Kählerian. The specification of an almost-Hermitian structure is equivalent to a reduction of the structure group of the tangent bundle to the group 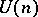 , where
, where 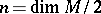 . Any non-degenerate differential
. Any non-degenerate differential  -form on a manifold
-form on a manifold 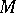 is the fundamental
is the fundamental  -form of some almost-Hermitian structure.
-form of some almost-Hermitian structure.
For references see Hermitian metric.
Hermitian structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hermitian_structure&oldid=33466