Green line
From Encyclopedia of Mathematics
An orthogonal trajectory of a family of level surfaces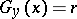 
, 
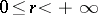, where 
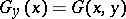is the Green function (of the Dirichlet problem for the Laplace equation) for a domain 
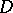in a Euclidean space 
, 
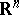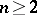, with a given pole 
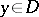. In other words, Green lines are integral curves in the gradient field 
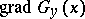. Generalizations also exist [2].
References
| [1] | N.S. [N.S. Landkov] Landkof, "Foundations of modern potential theory" , Springer (1972) pp. Chapt. 1 (Translated from Russian) |
| [2] | M. Brélot, G. Choquet, "Espaces et lignes de Green" Ann. Inst. Fourier , 3 (1952) pp. 199–263 |
How to Cite This Entry:
Green line. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Green_line&oldid=33454
Green line. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Green_line&oldid=33454
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article