Lebesgue number
From Encyclopedia of Mathematics
The Lebesgue number of an open covering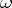 
of a metric space 
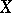is any number 
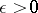such that if a subset 
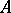of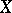 
has diameter 
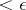, then 
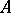is contained in at least one element of 
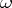. For any open covering (cf. Covering (of a set)) of a compactum there is at least one Lebesgue number; one can construct a two-element covering of the straight line for which there is no Lebesgue number.
The Lebesgue number of a system of closed subsets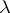 
of a metric space 
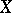is any number 
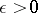such that if a set 
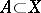of diameter 
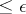intersects all the elements of some subsystem 
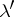of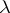 
, then the intersection of the elements of the system is not empty. Any finite system of closed subsets of a compactum has at least one Lebesgue number.
How to Cite This Entry:
Lebesgue number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue_number&oldid=33437
Lebesgue number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue_number&oldid=33437
This article was adapted from an original article by B.A. Pasynkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article