Bohl almost-periodic functions
A class of functions the typical property of which is that they can be uniformly approximated on the whole real axis by generalized trigonometric polynomials of the form
 |
where  are arbitrary integers, while
are arbitrary integers, while  are given real numbers. This class of functions contains the class of continuous
are given real numbers. This class of functions contains the class of continuous 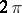 -periodic functions and is contained in the class of Bohr almost-periodic functions. P. Bohl specified several necessary and sufficient conditions for a function to be almost-periodic. In particular, any function of the type
-periodic functions and is contained in the class of Bohr almost-periodic functions. P. Bohl specified several necessary and sufficient conditions for a function to be almost-periodic. In particular, any function of the type
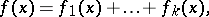 |
where each one of the functions 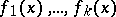 is continuous and periodic (with possibly different periods), is a Bohl almost-periodic function.
is continuous and periodic (with possibly different periods), is a Bohl almost-periodic function.
References
| [1] | P. Bohl, "Über die Darstellung von Funktionen einer Variabeln durch trigonometrische Reihen mit mehreren einer Variabeln proportionalen Argumenten" , Dorpat (1893) (Thesis) |
| [2] | P. Bohl, "Ueber eine Differentialgleichung der Störungstheorie" J. Reine Angew. Math. , 131 (1906) pp. 268–321 |
| [3] | B.M. Levitan, "Almost-periodic functions" , Moscow (1953) (In Russian) |
Comments
A very well-known reference for this kind of topic is [a1].
References
| [a1] | H. Bohr, "Almost periodic functions" , Chelsea, reprint (1947) (Translated from German) |
Bohl almost-periodic functions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bohl_almost-periodic_functions&oldid=33429