Resolvent set
From Encyclopedia of Mathematics
The set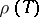 
of complex numbers 
, where 
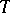is a linear operator in a Banach space, for which there is an operator 
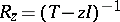which is bounded and has a dense domain of definition in 
. The set complementary to the resolvent set is the spectrum of the operator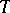 
(cf. Spectrum of an operator).
References
| [1] | F. Riesz, B. Szökevalfi-Nagy, "Leçons d'analyse fonctionelle" , Akad. Kiado (1952) |
Comments
I.e., 
is in the resolvent set of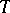 
if the range of 
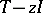is dense and 
has a continuous inverse. This inverse is often denoted by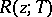 
, and it is called the resolvent (at 
) of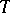 
.
References
| [a1] | K. Yosida, "Functional analysis" , Springer (1978) pp. 209ff |
| [a2] | M. Reed, B. Simon, "Methods of modern mathematical physics" , 1. Functional analysis , Acad. Press (1972) pp. 188, 253 |
How to Cite This Entry:
Resolvent set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Resolvent_set&oldid=33424
Resolvent set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Resolvent_set&oldid=33424
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article