Lebesgue summation method
From Encyclopedia of Mathematics
A method for summing trigonometric series. The series
 | (*) |
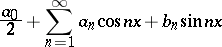is summable at a point 
by the Lebesgue summation method to the sum 
if in some neighbourhood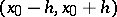 
of this point the integrated series
 |
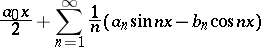converges and its sum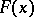 
has symmetric derivative at 
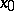equal to 
:
 |
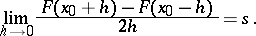The last condition can also be represented in the form
 |
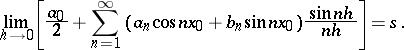The Lebesgue summation method is not regular, in the sense that it is not possible to sum every convergent trigonometric series (*) (see Regular summation methods), but if (*) is the Fourier series of a summable function 
, then it is summable almost-everywhere to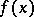 
by the Lebesgue summation method. The method was proposed by H. Lebesgue [1].
References
| [1] | H. Lebesgue, "Leçons sur les séries trigonométriques" , Gauthier-Villars (1906) |
| [2] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
How to Cite This Entry:
Lebesgue summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue_summation_method&oldid=33421
Lebesgue summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue_summation_method&oldid=33421
This article was adapted from an original article by I.I. Volkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article