Hermitian symmetric space

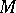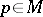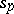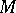A connected complex manifold with a Hermitian structure in which each point is an isolated fixed point of some holomorphic involutory isometry of . The component of the identity of the group 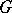of holomorphic isometries of 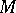acts transitively on 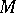. Let 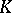be the isotropy subgroup of 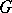relative to some point 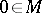. Then 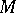is said to be of compact or non-compact type in accordance with the type of the globally symmetric Riemannian space 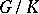. 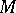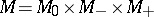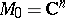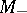Every Hermitian symmetric space is a direct product , where all the factors are simply-connected Hermitian symmetric spaces, and and 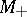are spaces of compact and non-compact type, respectively. Any Hermitian symmetric space of compact or non-compact type is simply connected and is a direct product of irreducible Hermitian symmetric spaces.

A non-compact irreducible Hermitian symmetric space is of the form 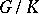, where 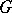is a connected non-compact simple Lie group with trivial centre and 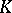is a maximal compact subgroup of 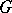having non-discrete centre. Compact irreducible Hermitian symmetric spaces are of the form 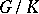, where 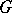is a connected compact simple Lie group with trivial centre and 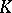is a maximal connected proper subgroup of 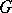having non-discrete centre.

A Hermitian symmetric space of non-compact type arises in the following way in the theory of functions of several complex variables. Let 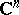be the -dimensional complex vector space. A bounded domain is defined as a connected bounded open subset of 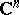. A bounded domain 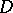is said to to be symmetric if every point 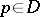is an isolated fixed point of some involutory holomorphic diffeomorphism of 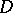onto itself. The following theorem holds: a) every bounded symmetric domain 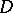equipped with the Bergman metric (see Bergman kernel function; Homogeneous bounded domain) is a Hermitian symmetric space of non-compact type, in particular, a bounded symmetric domain is necessarily simply connected; and b) let 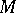be a Hermitian space of non-compact type, then there is a bounded symmetric domain 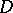and a holomorphic diffeomorphism of 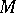onto .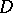

For references see Symmetric space.