Average
with weight 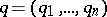 ,
, 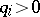 ,
, 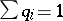 , of a set of real numbers
, of a set of real numbers 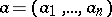
A variable
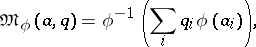 |
where 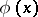 is a continuous strictly-monotone function on
is a continuous strictly-monotone function on 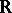 . When
. When 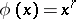 , one obtains
, one obtains
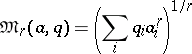 |
and, in particular, when 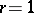 ,
, 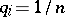 ,
, 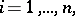
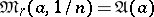 will be the arithmetic average of the numbers
will be the arithmetic average of the numbers  , while when
, while when 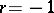 , it will be the harmonic average. The concepts of the geometric average
, it will be the harmonic average. The concepts of the geometric average 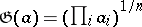 and the weighted geometric average
and the weighted geometric average
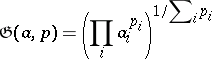 |
are introduced separately.
One of the basic results of the theory of averages is the inequality 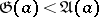 , except when all
, except when all 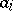 are equal to each other. Other results are:
are equal to each other. Other results are:
1) 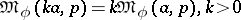 ;
;
2) 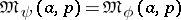 if and only if
if and only if 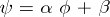 ,
, 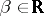 ,
, 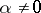 ;
;
3) 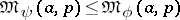 if and only if
if and only if 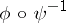 is a convex function; in particular
is a convex function; in particular 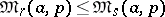 if
if 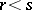 .
.
The concept of an average can be extended to infinite sequences under the assumption that the corresponding series and products converge, and to other functions. The following is such an example:
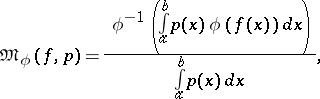 |
given the condition that  almost everywhere on the corresponding interval and that
almost everywhere on the corresponding interval and that 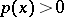 . Thus,
. Thus,
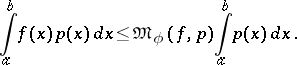 |
References
| [1] | G.H. Hardy, J.E. Littlewood, G. Pólya, "Inequalities" , Cambridge Univ. Press (1934) |
Comments
Instead of "average" the term "meanmean" is also quite often used: arithmetic mean, geometric mean, etc.
References
| [a1] | D.S. Mitrinović, "Analytic inequalities" , Springer (1970) |
| [a2] | D.S. Mitrinović, "Elementary inequalities" , Noordhoff (1964) |
Average. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Average&oldid=33369