Phase velocity vector
From Encyclopedia of Mathematics
The vector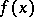 
originating at a point 
of the phase space 
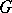of the autonomous system
 |
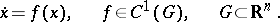Let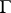 
be the phase trajectory of the system passing through a point 
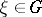; if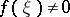 
, then the phase velocity vector 
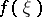is tangent to 
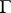and represents the instantaneous rate of the motion along 
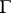of a representative point of the system at the moment of passing through the position 
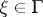. If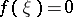 
, then 
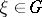is an equilibrium position.
References
| [1] | L.S. Pontryagin, "Ordinary differential equations" , Addison-Wesley (1962) (Translated from Russian) |
Comments
References
| [a1] | V.I. Arnol'd, "Geometrical methods in the theory of ordinary differential equations" , Springer (1983) (Translated from Russian) |
How to Cite This Entry:
Phase velocity vector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Phase_velocity_vector&oldid=33358
Phase velocity vector. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Phase_velocity_vector&oldid=33358
This article was adapted from an original article by N.Kh. Rozov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article