Curvature tensor

A tensor of type obtained by decomposing the curvature form in a local co-basis on a manifold . In particular, in a holonomic co-basis , , the components of the curvature tensor of an affine connection are expressed in terms of the Christoffel symbols of the connection and their derivatives:

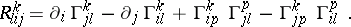In similar fashion one defines the curvature tensor for an arbitrary connection on a principal fibre space with structure Lie group in terms of a decomposition of the appropriate curvature form; this applies, in particular, to conformal and projective connections. It takes values in the Lie algebra of the group and is an example of a so-called tensor with non-scalar components.

For references see Curvature.