Metric tensor
basic tensor, fundamental tensor
A twice covariant symmetric tensor field 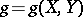 on an
on an  -dimensional differentiable manifold
-dimensional differentiable manifold 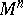 ,
, 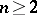 . The assignment of a metric tensor on
. The assignment of a metric tensor on 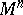 introduces a scalar product
introduces a scalar product  of contravariant vectors
of contravariant vectors 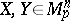 on the tangent space
on the tangent space 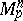 of
of 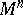 at
at 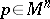 , defined as the bilinear function
, defined as the bilinear function 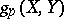 , where
, where 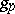 is the value of the field
is the value of the field 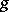 at the point
at the point 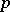 . In coordinate notation:
. In coordinate notation:
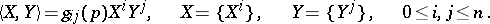 |
The metric in 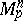 with this scalar product is regarded as infinitesimal for the metric of the manifold
with this scalar product is regarded as infinitesimal for the metric of the manifold 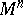 , which is expressed by the choice of the quadratic differential form
, which is expressed by the choice of the quadratic differential form
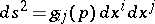 | (*) |
as the square of the differential of the arc length of curves in 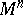 , going from
, going from 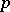 in the direction
in the direction 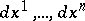 . With respect to its geometric meaning the form (*) is called the metric form or first fundamental form on
. With respect to its geometric meaning the form (*) is called the metric form or first fundamental form on 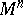 , corresponding to the metric tensor
, corresponding to the metric tensor 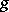 . Conversely, if a symmetric quadratic form (*) on
. Conversely, if a symmetric quadratic form (*) on 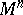 is given, then there is a twice covariant tensor field
is given, then there is a twice covariant tensor field 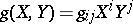 associated with it and whose corresponding metric form is
associated with it and whose corresponding metric form is 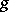 . Thus, the specification of a metric tensor
. Thus, the specification of a metric tensor  on
on 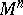 is equivalent to the specification of a metric form on
is equivalent to the specification of a metric form on 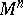 with a quadratic line element of the form (*). The metric tensor completely determines the intrinsic geometry of
with a quadratic line element of the form (*). The metric tensor completely determines the intrinsic geometry of 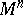 .
.
The collection of metric tensors 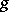 , and the metric forms defined by them, is divided into two classes, the degenerate metrics, when
, and the metric forms defined by them, is divided into two classes, the degenerate metrics, when 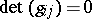 , and the non-degenerate metrics, when
, and the non-degenerate metrics, when  . A manifold
. A manifold 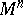 with a degenerate metric form (*) is called isotropic. Among the non-degenerate metric tensors, in their turn, are distinguished the Riemannian metric tensors, for which the quadratic form (*) is positive definite, and the pseudo-Riemannian metric tensors, when (*) has variable sign. A Riemannian (pseudo-Riemannian) metric introduced on
with a degenerate metric form (*) is called isotropic. Among the non-degenerate metric tensors, in their turn, are distinguished the Riemannian metric tensors, for which the quadratic form (*) is positive definite, and the pseudo-Riemannian metric tensors, when (*) has variable sign. A Riemannian (pseudo-Riemannian) metric introduced on 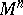 via a Riemannian (pseudo-Riemannian) metric tensor defines on
via a Riemannian (pseudo-Riemannian) metric tensor defines on 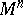 a Riemannian (respectively, pseudo-Riemannian) geometry.
a Riemannian (respectively, pseudo-Riemannian) geometry.
Usually a metric tensor, without special indication, means a Riemannian metric tensor; but if one wishes to stress that the discussion is about Riemannian and not about pseudo-Riemannian metric tensors, then one speaks of a proper Riemannian metric tensor. A proper Riemannian metric tensor can be introduced on any paracompact differentiable manifold.
References
| [1] | L.P. Eisenhart, "Riemannian geometry" , Princeton Univ. Press (1949) |
| [2] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [3] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
Comments
References
| [a1] | W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German) |
Metric tensor. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Metric_tensor&oldid=33342