Duffing equation

A second-order ordinary differential equation

(*)

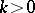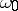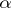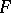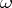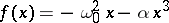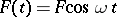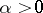where , , , , are constants. This equation is an important example of a system with one degree of freedom with a non-linear restoring force and damping, which executes forced oscillations under the effect of a harmonic external force . If one speaks of a rigid elastic force while if 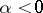one speaks of a soft force. G. Duffing [1] was the first to study the solutions of equation (*).

Solutions of Duffing's equation cannot be obtained in closed form. It has been proved that the equation has a large number of distinct periodic solutions. In equation (*), possible harmonic oscillations are with an amplitude 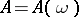which is a function of the frequency (an amplitude curve); to certain values of the frequency 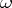there may correspond several types of oscillations with different amplitudes. Under certain conditions Duffing's equation yields subharmonic oscillations with frequencies , where is an integer. The solutions of equation (*) are often studied by the method of the small parameter.

References

[1]	G. Duffing, "Erzwungene Schwingungen bei veränderlicher Eigenfrequenz und ihre technische Bedeutung" , Vieweg (1918)
[2]	J.J. Stoker, "Nonlinear vibrations in mechanical and electrical systems" , Interscience (1950)
[3]	C. Hayashi, "Nonlinear oscillations in physical systems" , McGraw-Hill (1964)

References

[a1]	Ph. Holmes, "Non-linear oscillations, dynamical systems, and bifurcations of vector fields" , Springer (1983)