Limiting-amplitude principle
A method for uniquely reconstructing solutions of stationary equations by a limit transition, as 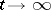 , of the amplitude of the solution of the corresponding non-stationary equation with zero initial data and a right-hand side of the form
, of the amplitude of the solution of the corresponding non-stationary equation with zero initial data and a right-hand side of the form 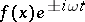 , periodic in
, periodic in 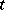 . If the limiting-amplitude principle holds, then the solution
. If the limiting-amplitude principle holds, then the solution 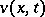 of the non-stationary problem described has, as
of the non-stationary problem described has, as 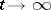 , the form
, the form
 | (*) |
where 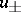 is the solution to the stationary equation, which describes stable oscillations.
is the solution to the stationary equation, which describes stable oscillations.
This principle was proposed at first [1] for the Helmholtz equation in 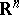 ,
,
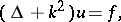 |
and it determines the same solution of this equation as the radiation conditions and the limit-absorption principle. Fulfillment of the limiting-amplitude principle has been investigated: for second-order equations with variable coefficients in the exterior of a bounded region (cf. [2], [3]); for the Helmholtz equation in certain regions with non-compact boundary (cf. [3], [4]); for the Cauchy–Poisson problem in a strip (cf. [5]); for certain higher-order equations (cf. [3], [6]); and for mixed problems in the exterior of a bounded region for equations and systems of equations of arbitrary order and with variable coefficients (cf. [7]). In the latter case the radiation and limit-absorption principles determine 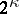 ,
,  , solutions to the stationary equation, while the limiting-amplitude principle determines only 2 of them. A statement of the limiting-amplitude principle that allows one to determine all
, solutions to the stationary equation, while the limiting-amplitude principle determines only 2 of them. A statement of the limiting-amplitude principle that allows one to determine all 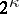 solutions has been given [8].
solutions has been given [8].
For the limiting-amplitude principle to hold it is necessary that 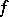 is orthogonal to all eigen functions of the stationary problem. Therefore the principle does not hold in bounded regions. Let
is orthogonal to all eigen functions of the stationary problem. Therefore the principle does not hold in bounded regions. Let 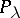 be the operator corresponding to the stationary problem, depending polynomially on the spectral parameter
be the operator corresponding to the stationary problem, depending polynomially on the spectral parameter 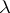 , obtained from the mixed problem for a non-stationary equation by replacing in the equation and boundary conditions the differentiation operator
, obtained from the mixed problem for a non-stationary equation by replacing in the equation and boundary conditions the differentiation operator 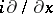 by
by 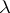 . The fulfillment of the limiting-amplitude principle for
. The fulfillment of the limiting-amplitude principle for 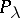 ,
, 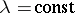 , is related to the possibility of analytic continuation of the kernel of the resolvent
, is related to the possibility of analytic continuation of the kernel of the resolvent 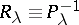 onto the continuous spectrum and to the smoothness (in
onto the continuous spectrum and to the smoothness (in 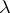 ) of this continuation (cf. [3], [7]). If the kernel
) of this continuation (cf. [3], [7]). If the kernel 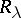 allows analytic continuation across the continuous spectrum and if one has appropriate estimates, as
allows analytic continuation across the continuous spectrum and if one has appropriate estimates, as 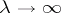 , then one can describe the asymptotics of the remainder
, then one can describe the asymptotics of the remainder 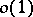 , as
, as 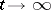 , in (*), and one can obtain asymptotic expansions, as
, in (*), and one can obtain asymptotic expansions, as 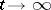 , of solutions of other non-stationary problems (cf. [2], [7]). The properties of
, of solutions of other non-stationary problems (cf. [2], [7]). The properties of 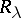 mentioned above have been obtained in [7] for mixed problems in the exterior of a bounded region for equations and systems of equations of arbitrary order.
mentioned above have been obtained in [7] for mixed problems in the exterior of a bounded region for equations and systems of equations of arbitrary order.
References
| [1] | A.N. Tikhonov, A.A. Samarskii, "On the radiation principle" Zh. Eksper. i Teoret. Fiz. , 18 : 2 (1948) pp. 243–248 (In Russian) |
| [2] | O.A. Ladyzhenskaya, "On the limiting-amplitude principle" Uspekhi Mat. Nauk , 12 : 3 (1957) pp. 161–164 (In Russian) |
| [3] | D.M. Eidus, "The principle of limiting amplitude" Russian Math. Surveys , 24 : 3 (1969) pp. 97–167 Uspekhi Mat. Nauk , 24 : 3 (1969) pp. 91–156 |
| [4] | A.G. Sveshnikov, "On the radiation principle" Dokl. Akad. Nauk SSSR , 73 : 5 (1950) pp. 917–920 (In Russian) |
| [5] | E.K. Isakova, "The limiting amplitude principle for the Cauchy–Poisson problem in a plane I" Differential Eq. , 6 : 1 (1970) pp. 45–55 Differentsial. Uravn. , 6 : 1 (1970) pp. 56–71 |
| [6] | V.P. Mikhailov, "Stabilizing the solution of a certain nonsteadystate boundary value problem" Proc. Steklov Inst. Math. , 91 (1969) pp. 103–116 Trudy Mat. Inst. Steklov. , 91 (1967) pp. 100–112 |
| [7] | B.R. Vainberg, "On the short wave asymptotic behaviour of solutions of stationary problems and the asymptotic behaviour as 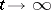 of solutions of non-stationary problems" Russian Math. Surveys , 30 : 2 (1975) pp. 1–58 Uspekhi Mat. Nauk , 30 : 2 (1975) pp. 3–55 of solutions of non-stationary problems" Russian Math. Surveys , 30 : 2 (1975) pp. 1–58 Uspekhi Mat. Nauk , 30 : 2 (1975) pp. 3–55 |
| [8] | B.R. Vainberg, "The limiting amplitude principle" Izv. Vyzov. Mat. , 2 (1974) pp. 12–23 (In Russian) |
Limiting-amplitude principle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Limiting-amplitude_principle&oldid=33291