Polynomial least deviating from zero

polynomial deviating least from zero

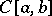An algebraic polynomial of degree , with leading coefficient 1, having minimal norm in the space or .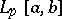

P.L. Chebyshev [1] proved that, among all polynomials of the form

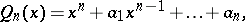(1)

there is exactly one, viz.

of minimal norm in 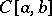, and that norm is

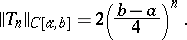The polynomial

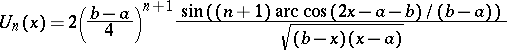is the unique polynomial deviating least from zero in 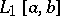(among all polynomials (1)), and its norm is

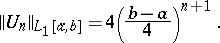In 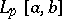, , there also exists a unique polynomial deviating least from zero; various properties of this polynomial are known (see [2], [5]).

The integral

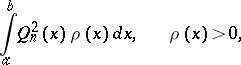(2)

considered for all polynomials (1), is minimal if and only if 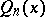, with respect to the weight function 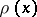, is orthogonal on 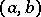to all polynomials of degree . If

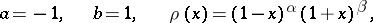where 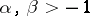, then the integral (2) is minimized by the Jacobi polynomial (cf. Jacobi polynomials) (if 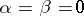by the Legendre polynomial; cf. Legendre polynomials) of degree with leading coefficient 1.

Among all trigonometric polynomials of the form

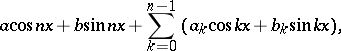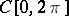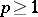where and are fixed, the polynomial of minimal norm in any of the spaces and (for an arbitrary ) is

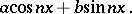References

[1]	P.L. Chebyshev, "Complete collected works" , 2 , Moscow-Leningrad (1947) pp. 23–51 (In Russian)
[2]	V.M. Tikhomirov, "Some problems in approximation theory" , Moscow (1976) (In Russian)
[3]	A.F. Timan, "Theory of approximation of functions of a real variable" , Pergamon (1963) (Translated from Russian)
[4]	G. Szegö, "Orthogonal polynomials" , Amer. Math. Soc. (1975)
[5]	S.M. Nikol'skii, "Quadrature formulas" , Hindushtan Publ. Comp. , London (1964) (Translated from Russian)
[6]	P.K. Suetin, "Classical orthogonal polynomials" , Moscow (1976) (In Russian)

Comments

The polynomials 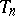and are called (normalized) Chebyshev polynomials of the first, respectively second, kind (cf. Chebyshev polynomials).

References

[a1]	I.P. Natanson, "Constructive function theory" , 2 , F. Ungar (1964–1965) pp. Chapt. 6 (Translated from Russian)
[a2]	T.J. Rivlin, "The Chebyshev polynomials" , Wiley (1974)
[a3]	M.J.D. Powell, "Approximation theory and methods" , Cambridge Univ. Press (1981)