Conductor of an integral closure
From Encyclopedia of Mathematics
The ideal of a commutative integral ring 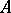 which is the annihilator of the
which is the annihilator of the 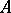 -module
-module 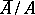 , where
, where 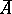 is the integral closure of
is the integral closure of 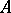 in its field of fractions. Sometimes the conductor is regarded as an ideal of
in its field of fractions. Sometimes the conductor is regarded as an ideal of 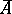 . If
. If 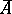 is an
is an 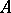 -module of finite type (e.g., if
-module of finite type (e.g., if 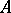 is a geometric ring), a prime ideal
is a geometric ring), a prime ideal 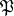 of
of 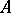 contains the conductor if and only if the localization
contains the conductor if and only if the localization 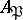 is not an integrally-closed local ring. In geometrical terms this means that the conductor determines a closed subscheme of the affine scheme
is not an integrally-closed local ring. In geometrical terms this means that the conductor determines a closed subscheme of the affine scheme 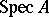 , consisting of the points that are not normal.
, consisting of the points that are not normal.
References
| [1] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) |
| [2] | O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975) |
How to Cite This Entry:
Conductor of an integral closure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conductor_of_an_integral_closure&oldid=33221
Conductor of an integral closure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Conductor_of_an_integral_closure&oldid=33221
This article was adapted from an original article by I.V. Dolgachev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article