Normal zero-dimensional cycle

cycle of index zero

A cycle 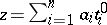such that 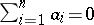. A cycle homologous to zero is always normal; the quotient group of the group of normal cycles by that of the cycles homologous to zero is called the reduced zero-dimensional homology group. For a connected complex the reduced group is zero, which is convenient in any kind of definition of acyclicity. A proper cycle 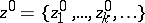is called normal if each of the cycles 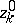is normal.