Euler function
From Encyclopedia of Mathematics
The arithmetic function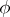 
whose value at 
is equal to the number of positive integers not exceeding 
and relatively prime to 
. The Euler function is multiplicative, that is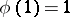 
and 
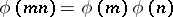for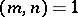 
. The function 
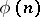satisfies the relations
 |
 |
 |
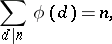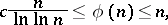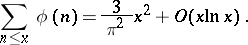It was introduced by L. Euler (1763).
References
| [1] | K. Chandrasekharan, "Introduction to analytic number theory" , Springer (1968) |
Comments
The function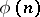 
can be evaluated by 
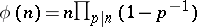, where the product is taken over all primes dividing 
, cf. [a1].
For a derivation of the asymptotic formula in the article above, as well as of the formula
 |
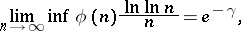where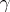 
is the Euler constant, see also [a1], Chapts. 18.4 and 18.5.
References
| [a1] | G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Oxford Univ. Press (1979) pp. Chapts. 5; 7; 8 |
How to Cite This Entry:
Euler function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler_function&oldid=33210
Euler function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Euler_function&oldid=33210
This article was adapted from an original article by S.A. Stepanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article