Strong differentiation of an indefinite integral
From Encyclopedia of Mathematics
Finding the strong derivative of an indefinite integral
 |
of a real-valued function 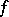 that is summable in an open subset
that is summable in an open subset 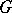 of
of  -dimensional Euclidean space, considered as a function of the interval
-dimensional Euclidean space, considered as a function of the interval 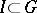 . If
. If
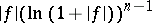 |
is summable on 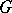 (in particular, if
(in particular, if  ,
, 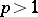 ), then the integral
), then the integral 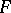 of
of 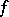 is strongly differentiable almost-everywhere on
is strongly differentiable almost-everywhere on 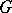 . For any
. For any 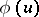 ,
, 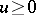 , that is positive, non-decreasing and such that
, that is positive, non-decreasing and such that
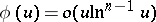 |
as 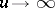 , there is a summable function
, there is a summable function 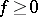 on
on 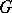 such that
such that 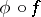 is also summable and such that the ratio
is also summable and such that the ratio 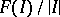 is unbounded at each
is unbounded at each 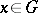 , as
, as 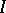 tends to
tends to  , that is,
, that is, 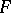 cannot be strongly differentiated.
cannot be strongly differentiated.
References
| [1] | B. Jessen, J. Marcinkiewicz, A. Zygmund, "Note on the differentiability of multiple integrals" Fund. Math. , 25 (1935) pp. 217–234 |
| [2] | S. Saks, "On the strong derivatives of functions of intervals" Fund. Math. , 25 (1935) pp. 235–252 |
| [3] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
| [4] | A. Zygmund, "Trigonometric series" , 2 , Cambridge Univ. Press (1988) |
Comments
References
| [a1] | A. Zygmund, "On the differentiability of multiple integrals" Fund. Math. , 23 (1934) pp. 143–149 |
How to Cite This Entry:
Strong differentiation of an indefinite integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strong_differentiation_of_an_indefinite_integral&oldid=33208
Strong differentiation of an indefinite integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strong_differentiation_of_an_indefinite_integral&oldid=33208
This article was adapted from an original article by T.P. Lukashenko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article