Functional separability

The property of two sets 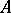and in a topological space 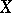requiring the existence of a continuous real-valued functi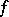on on 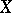such that the closures of the sets 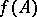and 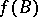(relative to the usual topology on the real line 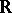) do not intersect. For example, a space is completely regular if every closed set is separable from each one-point set that does not intersect it. A space is normal if every two closed non-intersecting subsets of it are functionally separable. If every two (distinct) one-point sets in a space are functionally separable, then the space is called functionally Hausdorff. The content of these definitions is unchanged if, instead of continuous real-valued functions, one takes continuous mappings into the plane, into an interval or into the Hilbert cube.

References

[1]	A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian)
[2]	J.L. Kelley, "General topology" , Springer (1975)