Entropy of a measurable decomposition
From Encyclopedia of Mathematics
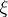of a space with a normalized measure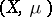 
A concept defined as follows. If the elements of 
having measure zero form in total a set of positive measure, then the entropy of 
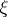is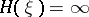 
; otherwise
 |
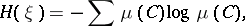where the sum is taken over all elements of 
of positive measure. The logarithm is usually to the base 2.
Comments
Instead of "measurable decomposition" the phrase "measurable partitionmeasurable partition" is often used, cf. [a1].
References
| [a1] | I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) (Translated from Russian) |
How to Cite This Entry:
Entropy of a measurable decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Entropy_of_a_measurable_decomposition&oldid=33192
Entropy of a measurable decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Entropy_of_a_measurable_decomposition&oldid=33192
This article was adapted from an original article by D.V. Anosov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article