Geodesic region
A connected set 
of points on a surface 
such that for each point 
there exists a disc 
with centre at 
such that 
has one of the following forms: 1) 
; 2) 
is a semi-disc of the disc; 3) 
is a sector of 
other than a semi-disc; or 4)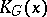 
consists of a finite number of sectors 
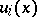of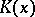 
with no common points except 
.
A point 
is called a regular interior point in the first case, a regular boundary point in the second, an angular point in the third, and a nodal point in the fourth case. A geodesic region that is compact in itself and has no nodal points is called a normal region. A normal region is either a closed surface or a surface with boundary consisting of a finite number of pairwise non-intersecting Jordan polygons.
A geodesic region may be considered as a metric space by introducing the so-called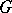 
-distance 
between two points 
and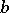 
(the greatest lower bound of the lengths of all rectifiable curves connecting 
and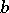 
and completely contained in 
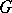). A rectifiable arc in 
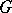with ends 
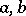is called a 
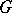-segment if it is the shortest connection between 
and 
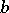in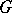 
. Single points are considered to be 
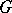-segments of length zero. For all points of a 
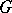-segment the equation 
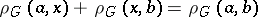is valid. A 
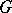-ray is a ray inside a geodesic region each partial arc of which is a 
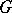-segment. A 
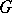-line consists of two rays with no points in common other than the origin, such that each arc contained in the line is a 
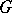-segment.
A geodesic region has a total curvature if and only if for any sequence of normal regions exhausting the geodesic region the total curvatures tend to a common value. If the Gaussian curvature of the domain is nowhere negative or if it is nowhere positive, then the domain has a total curvature. If the domain does not have a total curvature, then it is always possible to find an exhausting sequence of normal regions with total curvatures tending to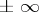 
. If the boundary of a complete geodesic region, homeomorphic to a closed half-plane, has only a finite number of angular points and if 
are the respective angles measured in the geodesic region, then the inequality
 |
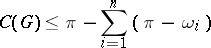is valid for the total curvature 
.
References
| [1] | S.E. Cohn-Vossen, "Kürzeste Wege und Totalkrümmung auf Flächen" Compos. Math. , 2 (1935) pp. 69–133 |
Comments
References
| [a1] | J. Cheeger, D.G. Ebin, "Comparison theorems in Riemannian geometry" , North-Holland (1975) |
Geodesic region. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Geodesic_region&oldid=33173