Spectral function, estimator of the

estimator of the spectral measure

A function of the observed values 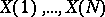of a discrete-time stationary stochastic process, used as an estimator of the spectral function 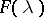. As an estimator of this function one often uses an expression of the form

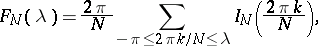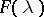where is the periodogram. Under fairly general smoothness conditions on , or under mixing conditions on the random process , this estimator turns out to be asymptotically unbiased and consistent.

The above estimator of is a special case of an estimator

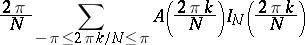of a function

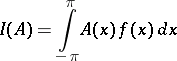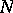of the spectral density . In particular, many estimators of the spectral density (cf. Spectral density, estimator of the) reduce to this form, where the function depends on the size of the sample and is concentrated about the point .

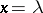References

[1]	D.R. Brillinger, "Time series. Data analysis and theory" , Holt, Rinehart & Winston (1975)
[2]	E.J. Hannan, "Multiple time series" , Wiley (1970)

References

[a1]	G.E.P. Box, G.M. Jenkins, "Time series analysis. Forecasting and control" , Holden-Day (1960)