Integral part
From Encyclopedia of Mathematics
entier, integer part of a (real) number 
The largest integer not exceeding 
. It is denoted by 
or by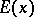 
. It follows from the definition of an integer part that 
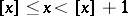. If 
is an integer,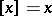 
. Examples: 
; 
, 
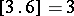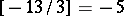. The integral part is used in the factorization of, for example, the number 
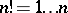, viz.
 |
where the product consists of all primes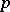 
not exceeding 
, and
 |
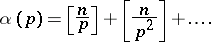The function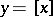 
of the variable 
is piecewise continuous (a step function) with jumps at the integers. Using the integral part one defines the fractional part of a number 
, denoted by the symbol 
and given by
 |
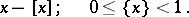The function 
is a periodic and piecewise continuous.
References
| [1] | I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian) |
How to Cite This Entry:
Integral part. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_part&oldid=33155
Integral part. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_part&oldid=33155
This article was adapted from an original article by B.M. Bredikhin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article