Pronormal subgroup

A subgroup 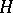of a group 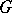satisfying the following condition: If 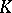is a subgroup in 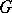conjugate with 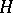, then 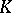is conjugate with 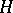in the subgroup generated by 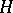and 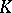(cf. Conjugate elements). Sylow subgroups in finite groups, as well as Hall and Carter subgroups in finite solvable groups, are pronormal (cf. Sylow subgroup; Hall subgroup; Carter subgroup). The concept of a pronormal subgroup is closely connected with that of an abnormal subgroup. Every abnormal subgroup is pronormal, and the normalizer of a pronormal subgroup (cf. Normalizer of a subset) is abnormal.

References

[1]	L.A. Shemetkov, "Formations of finite groups" , Moscow (1978) (In Russian)

References

[a1]	D.J.S. Robinson, "A course in the theory of groups" , Springer (1982)