Kronecker method
A method for factoring a polynomial with rational coefficients into irreducible factors over the field of rational numbers; proposed in 1882 by L. Kronecker [1]. Let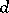 
be a common denominator of the coefficients of a polynomial 
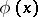. Then 
is a polynomial with integer coefficients; moreover, any factorization of 
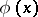into irreducible factors with rational coefficients leads to a factorization of 
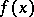into irreducible factors with integer coefficients, whose factors differ from the corresponding factors of 
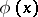only by constant factors, and vice versa.
Let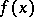 
be of degree 
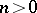and let 
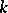be the largest natural number 
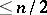. If 
is a factorization of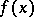 
into factors with integer coefficients, where the degree of 
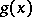does not exceed that of 
, then the degree of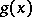 
is at most 
. Assigning to 
any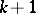 
distinct integer values 
, 
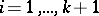, one obtains equalities
 |
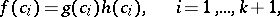where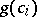 
and 
are integers. Thus, 
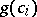divides 
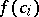. Choosing arbitrary divisors 
of the numbers 
, one obtains
 |
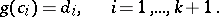The polynomial 
may now be determined from these equalities using the Lagrange interpolation formula, or, more simply, by the equations for the coefficients. It is then checked whether the polynomial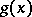 
found in this way divides 
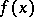. This construction and the subsequent test are carried out for all possible choices of divisors of the numbers 
.
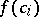Subsequently, the same procedure is applied to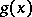 
and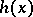 
, etc., until one obtains irreducible factors.
The Kronecker method involves cumbersome computations. It may be simplified by first lowering the degree of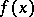 
by removing its rational roots (see [3]).
Example.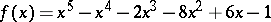 
(this is a polynomial with integer coefficients and without rational roots). If 
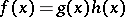, where the degree 
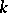of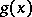 
is at most that of 
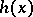, then 
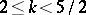, i.e. 
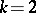. With 
, 
, 
one has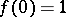 
; 
; 
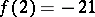. The divisors of these numbers are 
; 
; 
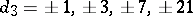. In all one has 
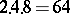combinations. Since two combinations 
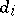that differ only in sign yield the two polynomials 
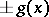, it will suffice to check only 
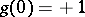. There remain 32 cases. Running through all these cases, one finds only one polynomial of degree 2 dividing 
: 
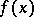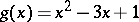. Hence 
. Both factors are irreducible (as polynomials of degrees 2 and 3, respectively, without rational roots).
References
| [1] | L. Kronecker, "Grundzüge einer arithmetischen Theorie der algebraischen Grössen" J. Reine Angew. Math. , 92 (1882) pp. 1–122 |
| [2] | L.Ya. Okunev, "Higher algebra" , Moscow (1937) (In Russian) |
| [3] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
Comments
References
| [a1] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) |
Kronecker method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kronecker_method&oldid=33142