Kirby calculus

Kirby moves

A set of moves between different surgery presentations of a -manifold.

W.B.R. Lickorish [a3] and A.D. Wallace [a4] showed that any orientable -manifold may be obtained as the result of surgery on some framed link in the -sphere.

A framed link is a finite, disjoint collection of smoothly embedded circles, with an integer (framing) assigned to each circle. R. Kirby [a2] described two operations (the calculus) on a framed link and proved that two different framed links, 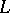and 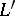, yield the same -manifold if and only if one can pass from to 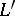by a sequence of these operations.

1) Blow-up: One may add or subtract from 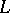an unknotted circle with framing 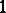or 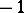, which is separated from the other circles by an embedded -sphere.

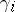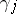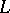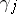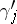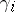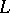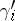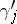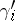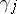2) Handle slide: Given two circles and in , one may replace with obtained as follows. First, push off itself (missing ) using the framing to get . Then, let be a band sum of with . Framing on 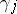is changed by taking the sum of framings on 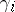and on 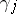with 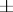algebraic linking number of 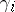with .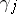

R.P. Fenn and C.P. Rourke [a1] proved that these operations are equivalent to a 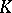-move, where links 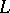and 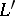are identical except in a part where an arbitrary number of parallel strands of 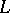are passing through an unknot 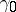with framing 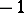(or 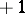). In the link 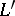the unknot 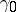disappears and the parallel strands of 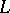are given one full right-hand (respectively, left-hand) twist.

References

[a1]	R.P. Fenn, C.P. Rourke, "On Kirby's calculus of links" Topology , 18 (1979) pp. 1–15
[a2]	R. Kirby, "A calculus for framed links in 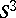" Invent. Math. , 45 (1978) pp. 35–56
[a3]	W.B.R. Lickorish, "A representation of orientable combinatorial -manifolds" Ann. Math. , 76 (1962) pp. 531–540
[a4]	A.H. Wallace, "Modification and cobounding manifolds" Canad. J. Math. , 12 (1960) pp. 503–528