Bohr almost-periodic functions

uniform almost-periodic functions

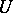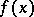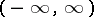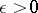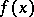The class -a.-p. of almost-periodic functions. The first definition, which was given by H. Bohr [1], is based on a generalization of the concept of a period: A continuous function on the interval is a Bohr almost-periodic function if for any there exists a relatively-dense set of -almost-periods of this function (cf. Almost-period). In other words, is 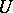-almost-periodic (or 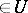-a.-p.) if for any 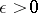there exists an 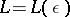such that in each interval of length 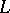there exists at least one number such that

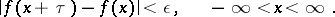If 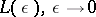, is bounded, a Bohr almost-periodic function 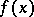becomes a continuous periodic function. Bochner's definition (cf. Bochner almost-periodic functions), which is equivalent to Bohr's definition, is also used in the theory of almost-periodic functions. Functions in the class of 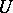-almost-periodic functions are bounded and uniformly-continuous on the entire real axis. 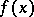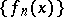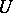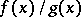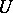The limit of a uniformly-convergent sequence of Bohr almost-periodic functions belongs to the class of -almost-periodic functions; this class is invariant with respect to arithmetical operations (in particular the Bohr almost-periodic function is -almost-periodic, under the condition

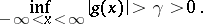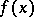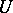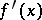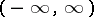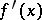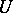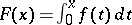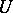If is -almost-periodic and if is uniformly continuous on , then is -almost-periodic; the indefinite integral is -almost-periodic if 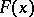is a bounded function.

References

[1]	H. Bohr, "Zur Theorie der fastperiodischen Funktionen I" Acta Math. , 45 (1925) pp. 29–127
[2]	B.M. Levitan, "Almost-periodic functions" , Moscow (1953) (In Russian)

Comments

Bohr's treatise [a1] is a good reference. An up-to-date reference is [a2].

References

[a1]	H. Bohr, "Almost periodic functions" , Chelsea, reprint (1947) (Translated from German)
[a2]	C. Corduneanu, "Almost periodic functions" , Wiley (1968)