Gradient dynamical system

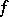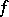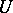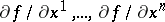A flow (continuous-time dynamical system) given by the gradient of a smooth function on a smooth manifold. Direct differentiation of yields a covariant vector (e.g. in the finite-dimensional case in a coordinate neighbourhood with local coordinates this is the vector with components ), while the phase velocity vector is a contravariant vector. The passage from the one to the other is realized with the aid of a Riemannian metric, and the definition of a gradient dynamical system depends on the choice of the metric (as well as on 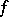); the phase velocity vector is often taken with the opposite sign. In the given example the gradient dynamical system in the domain 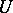is described by the system of ordinary differential equations

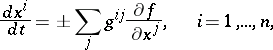where the coefficients 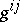form a matrix inverse to the matrix of coefficients 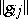of the metric tensor; it is understood that in all equations the right-hand side is taken with the same "plus" or "minus" sign. A gradient dynamical system is often understood to mean a system of a somewhat more general type [1].

References

[1]	S. Smale, "On gradient dynamical systems" Ann. of Math. (2) , 74 : 1 (1961) pp. 199–206