Bicategory(2)

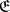A category in which subcategories of epimorphisms and of monomorphisms 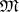have been distinguished such that the following conditions are met:

1) all morphisms 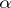in are decomposable into a product 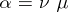, where , ;

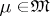2) if 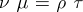, where 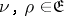, , 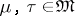then there exists an isomorphism 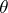such that 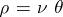, and ;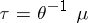

3) 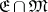coincides with the class of isomorphisms in the category .

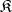The epimorphisms in 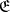(the monomorphisms in 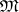) are called the permissible epimorphisms (monomorphisms) of the bicategory.

The concept of a bicategory axiomatizes the possibility of a decomposition of an arbitrary mapping into a product of a surjective and an injective mapping. The category of sets, the category of sets with a marked point and the category of groups are bicategories with a unique bicategorical structure. In the category of all topological spaces and in the category of all associative rings there are proper classes of different bicategorical structures.

References

[1]	M.Sh. Tsalenko, E.G. Shul'geifer, "Fundamentals of category theory" , Moscow (1974) (In Russian)

Comments

In the literature there has been much confusion about the terms bicategory and -category. Usually, bicategory is understood to mean "generalized 2-category" , and a bicategory as defined above is called, e.g., "bicategory in the sense of Isbell" .

In this Encyclopaedia the term bicategory is always used as defined above.