Differential parameter
differentiator
The joint differential invariant of one or more functions and the metric tensor 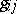 of a Riemannian geometry.
of a Riemannian geometry.
The first-order differential parameter (or simply differential parameter) of a function 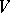 is the square of its gradient:
is the square of its gradient:
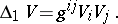 |
The first-order mixed differential parameter of two functions 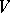 and
and 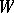 is the scalar product of their gradients
is the scalar product of their gradients
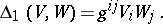 |
In three-dimensional Euclidean space and with respect to a Cartesian rectangular coordinate system these differential parameters are given by the formulas
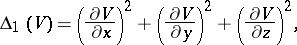 |
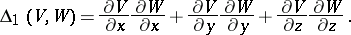 |
The second-order differential parameter (or second differential parameter) of a function is the divergence of its gradient:
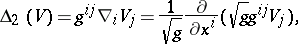 |
where 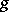 is the determinant of the matrix
is the determinant of the matrix 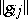 . In three-dimensional Euclidean space and with respect to a Cartesian rectangular coordinate system, the second differential parameter is given by the formula
. In three-dimensional Euclidean space and with respect to a Cartesian rectangular coordinate system, the second differential parameter is given by the formula
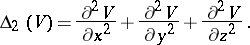 |
Differential parameters were first introduced by G. Lamé [1] in Euclidean geometry. E. Beltrami [2] must be credited with generalizing this concept. The differential parameters are therefore sometimes called Lamé or Beltrami differential parameters.
References
| [1] | G. Lamé, "Leçons sur les coordonnées curvilignes et leurs diverses applications" , Paris (1958) |
| [2] | E. Betrami, "Ricerche di analisi applicate alla geometria" G. Mat. Battaglini , 2–3 (1864–1865) |
| [3] | V.F. Kagan, "Foundations of the theory of surfaces in a tensor setting" , 1–2 , Moscow-Leningrad (1947–1948) (In Russian) |
| [4] | V.I. Shulikovskii, "Classical differential geometry in a tensor setting" , Moscow (1963) (In Russian) |
Comments
References
| [a1] | J.J. Stoker, "Differential geometry" , Wiley (Interscience) (1969) |
Differential parameter. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Differential_parameter&oldid=33103