Pseudo-basis

of a topological space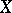

A family of sets open in 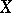and such that each point of 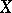is the intersection of all elements in the family containing it. A pseudo-basis exists only in spaces all singletons of which are closed (i.e. in 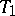-spaces). If a 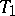-space with basis 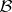is endowed with a stronger topology, then 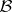is no longer a basis of the new topological space but remains a pseudo-basis of it. In particular, a discrete space of the cardinality of the continuum, which does not have a countable basis, has a countable pseudo-basis. However, for Hausdorff compacta (i.e. compact Hausdorff spaces) the presence of a countable pseudo-basis implies the existence of a countable basis.

References

[1]	A.V. Arkhangel'skii, V.I. Ponomarev, "Fundamentals of general topology: problems and exercises" , Reidel (1984) (Translated from Russian)

Comments

The term pseudo-basis is also used in two other ways, as follows.

A collection of non-empty open sets (in a topological space 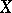) such that every non-empty open set of 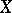contains one of these is also sometimes called a pseudo-basis, although the term 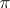-basis is favoured nowadays.

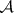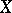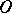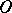Another use of "pseudo-basis" is for a collection of subsets of a topological space such that for every open set and every point of there is an element 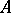of 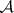such that

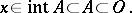Hence a topological space is regular (cf. Regular space) if and only if it has a closed pseudo-basis (in the second sense).