Gauss-Bonnet theorem
The total curvature 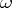 of a two-dimensional compact Riemannian manifold
of a two-dimensional compact Riemannian manifold 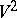 , closed or with boundary, and the rotation
, closed or with boundary, and the rotation  of its smooth boundary
of its smooth boundary 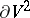 are connected with the Euler characteristic
are connected with the Euler characteristic 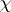 of
of 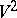 by the relation
by the relation
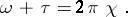 |
Here
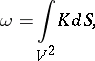 |
where 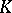 is the Gaussian curvature and
is the Gaussian curvature and  is the area element;
is the area element;
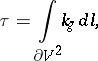 |
where 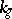 is the geodesic curvature and
is the geodesic curvature and 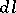 is the line element of the boundary. The Gauss–Bonnet theorem is also valid for a manifold with a piecewise-smooth boundary; in that case
is the line element of the boundary. The Gauss–Bonnet theorem is also valid for a manifold with a piecewise-smooth boundary; in that case
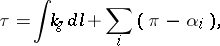 |
where  is the rotation of the boundary at a vertex. The theorem is valid, in particular, on regular surfaces in
is the rotation of the boundary at a vertex. The theorem is valid, in particular, on regular surfaces in 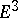 . The Gauss–Bonnet theorem was known to C.F. Gauss [1]; it was published by O. Bonnet [2] in a special form (for surfaces homeomorphic to a disc).
. The Gauss–Bonnet theorem was known to C.F. Gauss [1]; it was published by O. Bonnet [2] in a special form (for surfaces homeomorphic to a disc).
For a non-compact complete manifold 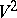 without boundary, an analogue of the Gauss–Bonnet theorem is the Cohn-Vossen inequality [3]:
without boundary, an analogue of the Gauss–Bonnet theorem is the Cohn-Vossen inequality [3]:
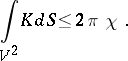 |
The Gauss–Bonnet theorem and the given inequality are also valid for convex surfaces and two-dimensional manifolds of bounded curvature.
The Gauss–Bonnet theorem can be generalized to even-dimensional compact Riemannian manifolds  , closed or with boundary:
, closed or with boundary:
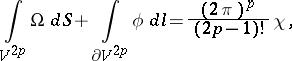 |
where 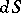 ,
, 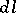 denote the volume elements in
denote the volume elements in 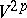 and
and  , while
, while  is some polynomial in the components of the curvature tensor of
is some polynomial in the components of the curvature tensor of 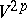 , and
, and 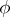 is some polynomial in the components of the curvature tensor and the coefficients of the second fundamental form of
is some polynomial in the components of the curvature tensor and the coefficients of the second fundamental form of  [4]. The Gauss–Bonnet theorem has also been generalized to Riemannian polyhedra [5]. Other generalizations of the theorem are connected with integral representations of characteristic classes by parameters of the Riemannian metric [4], [6], [7].
[4]. The Gauss–Bonnet theorem has also been generalized to Riemannian polyhedra [5]. Other generalizations of the theorem are connected with integral representations of characteristic classes by parameters of the Riemannian metric [4], [6], [7].
References
| [1] | C.F. Gauss, , Werke , 8 , K. Gesellschaft Wissenschaft. Göttingen (1900) |
| [2] | O. Bonnet, J. École Polytechnique , 19 (1848) pp. 1–146 |
| [3] | S.E. Cohn-Vossen, "Some problems of differential geometry in the large" , Moscow (1959) (In Russian) |
| [4] | V.A. Sharafutdinov, "Relative Euler class and the Gauss–Bonnet theorem" Siberian Math. J. , 14 : 6 (1973) pp. 930–940 Sibirsk Mat. Zh. , 14 : 6 pp. 1321–1635 |
| [5] | C.B. Allendörfer, A. Weil, "The Gauss–Bonnet theorem for Riemannian polyhedra" Trans. Amer. Math. Soc. , 53 (1943) pp. 101–129 |
| [6] | J. Eells, "A generalization of the Gauss–Bonnet theorem" Trans. Amer. Math. Soc. , 92 (1959) pp. 142–153 |
| [7] | L.S. Pontryagin, "On a connection between homologies and homotopies" Izv. Akad. Nauk SSSR Ser. Mat. , 13 (1949) pp. 193–200 (In Russian) |
Comments
References
| [a1] | M. Spivak, "A comprehensive introduction to differential geometry" , 5 , Publish or Perish (1975) pp. 1–5 |
Gauss-Bonnet theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss-Bonnet_theorem&oldid=33081