Torsion-free module
From Encyclopedia of Mathematics
A module  over a ring
over a ring  without divisors of zero, such that the equality
without divisors of zero, such that the equality  , where
, where  ,
,  , implies
, implies 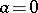 or
or  . Examples of such (left) modules are the ring
. Examples of such (left) modules are the ring 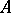 itself and all its non-zero left ideals. A submodule of a torsion-free module and also the direct sum and direct product of torsion-free modules are torsion-free modules. If
itself and all its non-zero left ideals. A submodule of a torsion-free module and also the direct sum and direct product of torsion-free modules are torsion-free modules. If  is commutative, then for any module
is commutative, then for any module 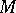 there is a torsion submodule
there is a torsion submodule
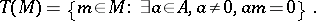 |
In this case the quotient module 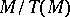 is torsion-free.
is torsion-free.
Comments
More generally, for any associative ring 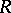 a left
a left  -module
-module  is called torsion-free if for
is called torsion-free if for  ,
, 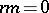 for a regular element
for a regular element  implies
implies  . Cf. Torsion submodule for more details and some references.
. Cf. Torsion submodule for more details and some references.
How to Cite This Entry:
Torsion-free module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Torsion-free_module&oldid=33072
Torsion-free module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Torsion-free_module&oldid=33072
This article was adapted from an original article by L.V. Kuz'min (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article