Irregular singular point
A concept that arose in the analytic theory of linear ordinary differential equations. Let 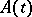 be an
be an 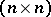 -matrix that is holomorphic in a punctured neighbourhood of
-matrix that is holomorphic in a punctured neighbourhood of 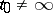 and that has a singularity at
and that has a singularity at  .
.
The point 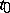 is then called a singular point of the system
is then called a singular point of the system
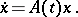 | (*) |
There are two non-equivalent definitions of an irregular singular point. According to the first one, 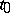 is called an irregular singular point of (*) if
is called an irregular singular point of (*) if 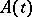 has a pole of order greater than one at
has a pole of order greater than one at 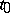 (cf. Analytic theory of differential equations, as well as [2]). According to the second definition,
(cf. Analytic theory of differential equations, as well as [2]). According to the second definition, 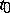 is called an irregular singular point of (*) if there is no number
is called an irregular singular point of (*) if there is no number 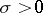 such that every solution
such that every solution 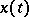 grows not faster than
grows not faster than 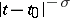 as
as 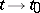 along rays (cf. [3]). The case
along rays (cf. [3]). The case 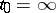 can be reduced to the case
can be reduced to the case  by the transformation
by the transformation 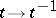 . An irregular singular point is sometimes called a strongly-singular point (cf., e.g., Bessel equation). In a neighbourhood of an irregular singular point the solutions admit asymptotic expansions; these were studied by H. Poincaré for the first time [1].
. An irregular singular point is sometimes called a strongly-singular point (cf., e.g., Bessel equation). In a neighbourhood of an irregular singular point the solutions admit asymptotic expansions; these were studied by H. Poincaré for the first time [1].
References
| [1] | H. Poincaré, "Sur les intégrales irrégulières des équations linéaires" Acta Math. , 8 (1886) pp. 295–344 |
| [2] | W. Wasov, "Asymptotic expansions for ordinary differential equations" , Interscience (1965) |
| [3] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) pp. Chapts. 13–17 |
Irregular singular point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Irregular_singular_point&oldid=33054